Mathematical Derivation of Analogical Gates
Analogical Gate derivation
The first investigation into analogical gates defined on [-1,1] was performed by Badreddin [@badreddin]. While the analogical gates derived in this paper follow the idea of [@badreddin] that the gates should be point symmetric, they have a different description that adheres closer to the behavior of their binary counterparts and is less nonlinear. The derivation of these new analogical gates is a two-step process:
-
extend the binary AND and OR to [0,1] using t-norms and s-norms respectively
-
extend the t-norms and s-norms to [-1,1] such that monotony is maintained and the resulting gates are point symmetric.
T-norms and s-norms can be understood as multivalued extensions of binary logic. Since the values between zero and one are not uniquely defined by binary logic there are multiple possible t-norms and s-norms. To avoid jerky motion these norms should be smooth. Furthermore, they should not introduce unnecessary nonlinearities. These considerations have led to the choice of the product t-norm and s-norm.
\[\begin{split} \textnormal{Product t-norm}~ \top_{Prod}(a,b) &= a b \\ \textnormal{Product s-norm}~ \bot_{Prod}(a,b) &= a+b-ab \\ \end{split}\]where \(a\) and \(b\) are input values defined on [0,1]. The simplest way to achieve the desired extension specified in B) is to multiply the norms with \(sign(a+b)\). However this produces a nonsmooth gate since the sign function is not smooth at zero. Since smoothness is a desired property of the gates, the sign function was smoothed using the tangens hyperbolicus. This results in the final description
\[\begin{split} AND(a,b)&=ab\frac{\tanh((a+b)/\lambda)}{\tanh(2/\lambda)}\\ OR(a,b)&=a+b-ab\frac{\tanh((a+b)/\lambda)}{\tanh(2/\lambda)} \end{split}\]where \(a\) and \(b\) are defined on [-1,1] and \(\lambda\) is the smoothing magnitude. The factor \(\tanh(2/\lambda)\) is used to ensure that \(AND(1,1)=OR(1,1)=1\). A contour plot of both functions can be below
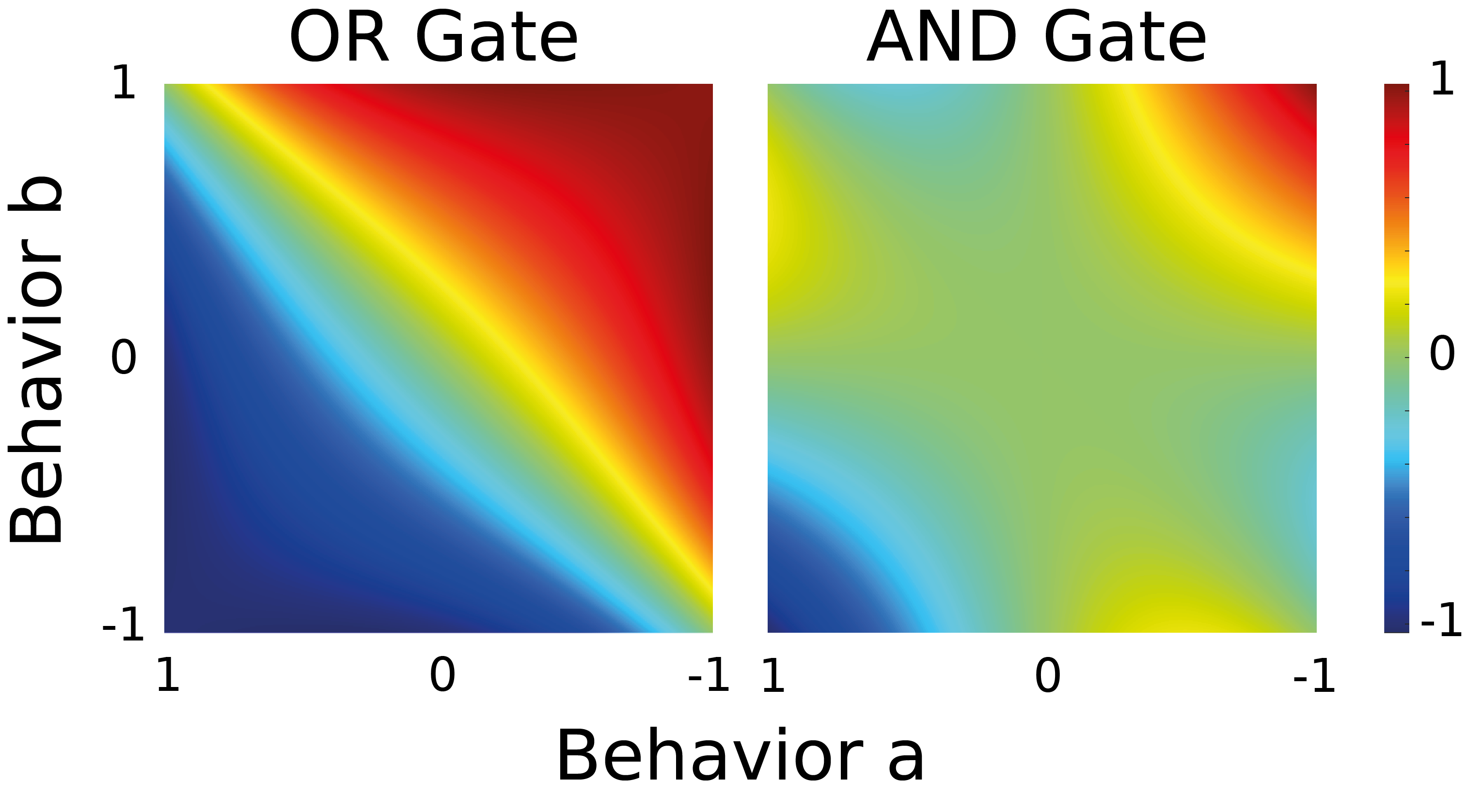
While a bigger \(\lambda\) leads to a smoother gate behavior, it also results in a slight deviation from the boundary values. For example \(OR_{\lambda=0.5}(1,0.1)\) is only 0.973 instead of 1.0. In practice, a smoothing magnitude of \(\lambda=1\) seems to be a good compromise. For the rest of this article, we will assume that all gates use a smoothing magnitude of \(\lambda=1\).
Since more complex circuits might require negation, a NOT operation can also be defined:
\[NOT(a)= (1-|a|)\frac{\tanh(a/\lambda)}{\tanh(1/\lambda)}\]Where \(\lambda\) is again the smoothing magnitude.
While this set of gates is already very expressive, they offer no way to map the input pairs (-1,-1) and (1,1) to the same nonzero value. This means it is not possible to implement rules which behave the same for negative and positive signs. For this, an additional gate is required.
For this purpose we proposed the AMP or AMPLIFICATION gate. Its simplest implementation is a multiplication:
\[AMP(a,b)=ab\]